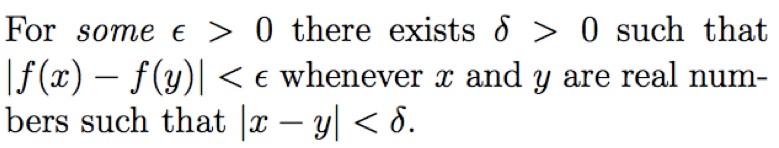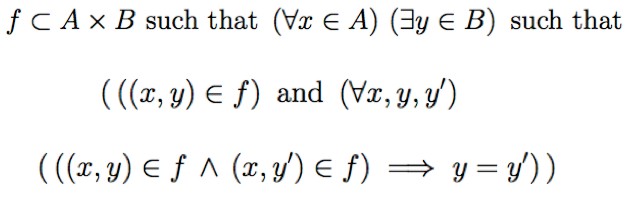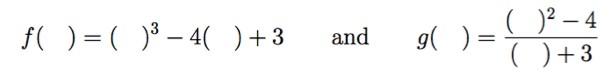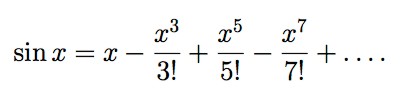Paul Zorn, St. Olaf College
Part II: Mathematics in Literature
Part III: What Is Mathematics?
Part IV: Mathematical Language: Learning from Barbie
On, then, to mathematical communication with our students and in our classrooms. I’ll sometimes refer specifically to textbooks. But I think that the same general principles apply, mutatis mutandis, to the larger project of communicating mathematics to non-specialists. Or, as Thurston put it, attempting to convey ideas to people who don’t already know them.
Communication with fellow specialists in a mathematical area seems to me to pose almost entirely different expository problems to those of non-specialist communication. I’ll have nothing more to say about this, except to opine that mistaking the one sort of communication with the other can, and often does, lead us into all sorts of error and confusion.
Back, for a moment, to the children’s doll Barbie, who raised mathematicians’ eyebrows some years ago. A small fraction of Teen Talk Babies, released in 1992, included “Math class is tough!” in their four-sentence linguistic repertoires. Protests followed, and the offending utterance was expunged.
Let’s reject right now the clearly offensive suggestion that math class is uniquely, or even especially, tough for Barbie’s target audience. Still, perhaps Barbie had a point. Math classes are often tough, and not just for bizarrely elongated plastic effigies.
Learning anything deep and difficult will always be challenging, to a degree proportional to, or at least monotonic in, the power and subtlety of the ideas involved. Perhaps less obvious is that “math class” may be tough for reasons connected to the nature of mathematics itself, and especially for students first seriously encountering theory and proofs. The villain, and the hero, is the special language of mathematics.
That we mathematicians use language in unusually precise and complex ways is hardly surprising: Communicating technical ideas and fine distinctions naturally requires extra linguistic effort. I suspect, though, that we underappreciate how formidable students often find it to parse correctly the mathematical sentences they meet in, say, a first course in real analysis. This is so even if we eschew special symbols like ∀ and ∃. Here, for instance, is one condition that might apply to a function f: R → R:
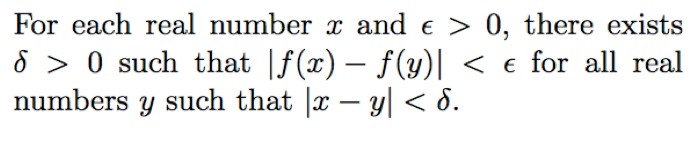Here’s another: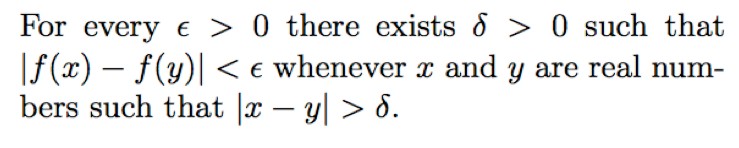 
It’s “obvious” (there’s another loaded and overused word) to an experienced analyst that these conditions describe continuity and uniform continuity of f, respectively. Other mathematicians, even if they’ve forgotten the lingo, have learned from experience to keep their eyes and inner ears tuned to just this sort of subtle variation from condition to condition, and so will quickly puzzle out what’s at stake. Mathematicians realize, too, that the words “each” and “every’” mean the same thing in these contexts, and that the word “whenever” here signals universal quantification, and has nothing to do with time.
Few students in my experience know such things instinctively or master them without hard work. Nor, in my experience, do even highly trained professionals in language-intensive areas like English literature find such sentences easy to parse—let alone understand. On the contrary, my academic colleagues in the arts and humanities usually marvel at the complexity and sensitivity to word order of sentences we routinely ask mathematics students to process.
Struggling with mathematical language is undeniably tough for students, but doing so is essential to real mathematical understanding and communication. One pedagogical technique I’ve found effective is to challenge students to find meaning in slightly perturbed or ostensibly incorrect versions of definitions like those above. What, for instance, is meant by the following condition on a function f: R → R?
Or this?
Let’s look at a few more instances of where communication issues arise in mathematics teaching and learning. Some glitches arise when words or phrases more or less familiar from everyday speech, like these—
- limit
- approaches
- countable
- any
- or
- almost all
- real
- imaginary
- unique
- point
- continuous
- smooth
- derivative
- differential
- integral
- measure
- space
- normal family
- inner function
- transcendental
are used in different or more precise ways in mathematics (see “The Mathematical Vocabulary Problem“). Fair enough; every field has its measure of technical language, and we wouldn’t get far without it.
But some difficulties in communication arise because we mathematicians sometimes use language ambiguously, if not downright wrongly. The fact that we often confess, a bit flippantly, to “abuse of language” or “abuse of notation” may make us feel better, but we’re still guilty.
One setting in which this occurs, especially regrettably, is in respect to functions, equations, and uses of the equals sign. Here’s an excerpt from the very first page of a still-in-print single-variable calculus textbook:
Such language, common as it is, obscures several important distinctions: between functions and their values; between functions and algebraic rules that define them; and between stipulated assignment and asserted equality. And there’s more to come. Students condemned to use this textbook will soon meet functional expressions like these:
each of which could lure an unwary (but careful) student into a morass of misunderstanding. How could a published author be so careless?
OK, it’s confession time: I wrote those words myself; they appear on page 1 of Volume 1 of my calculus text, Calculus from Graphical, Numerical, and Symbolic Points of View, with Arnie Ostebee.
Here’s another true confession: I’m not sorry I wrote those things. In the real world, authors and teachers and speakers have continually (or do I mean “continuously”?) to compromise between friendly but possibly vague informality on the one hand, and meticulous but possibly pedantic formality on the other. In my opinion, mathematically young students need to be guided carefully, but gently and over considerable time, from the former style to the latter.
Or one could introduce the impeccably correct definition of a function f as a special sort of subset of a Cartesian product:
(Thanks to Bonnie Gold for this formulation, and for an interesting discussion of these and related matters in an article called “How Your Philosophy of Mathematics Impacts Your Teaching!”, originally published in the MAA’s College Mathematics Journal, and reprinted in The Best Writing on Mathematics 2012, published by Princeton University Press, about which more soon.)
Presenting this definition to beginning calculus students would be unwise; this sort of correctness can be its own impediment to understanding. Doing so would also violate the one cardinal rule I think I’ve learned, very slowly, over many years of teaching:
Don’t answer questions students aren’t capable of asking.
A placeholder notation, like this—
may offer, despite its slightly odd appearance, a more accessible approach to some aspects of function definition, and it can help point to aspects of what variables are all about. Susanna Epp has written interestingly about this and many related issues in various places, including the American Mathematical Monthly and the same Best Writing on Mathematics 2012 compendium just alluded to (see “Variables in Mathematics Education”).
[To rehabilitate myself a bit as an author, let me add that some similar expressions appear on page 7 of my text with Ostebee.]Ahead for calculus students lie even rougher symbolic waves, in expressions like this:
There will be time to run those rapids when we reach them.
Part V: Rule Books and Tour Guides: Two Live Questions
Part VI: Lessons from History
Part VII: Valuing Communication